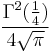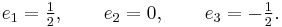Lemniscatic elliptic function
In mathematics, and in particular the study of Weierstrass elliptic functions, the lemniscatic case occurs when the Weierstrass invariants satisfy g2=1 and g3=0. This page follows the terminology of Abramowitz and Stegun; see also the equianharmonic case.
In the lemniscatic case, the minimal half period 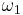 is real and equal to
is real and equal to
where 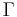 is the Gamma function. The second smallest half period is pure imaginary and equal to
is the Gamma function. The second smallest half period is pure imaginary and equal to 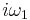 . In more algebraic terms, the period lattice is a real multiple of the Gaussian integers.
. In more algebraic terms, the period lattice is a real multiple of the Gaussian integers.
The constants 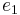 ,
, 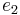 and
and 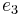 are given by
are given by
The case g2=a, g3=0 may be handled by a scaling transformation. However, this may involve complex numbers. If it is desired to remain within real numbers, there are two cases to consider: a>0 and a<0.
See also
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 18", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 658, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_658.htm.